Earlier today I set you three problems from a maths competition for Martian schoolchildren. By Martian, I mean Hungarian.
In the mid-twentieth century, a generation of outstanding mathematicians and physicists from Hungary were humorously called Martians, as their intelligence was from another planet.
Here are the puzzles again with solutions.
1. Curb your enthusiasm (Ages 13/14)
On an island, every resident is either half-hearted or enthusiastic. A visitor from a distant land was invited for dinner by a group of 10 residents. After dinner, the visitor asked all 10 members of the group about the number of enthusiastic inhabitants within their group.
She received the following answers: 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Knowing that the answers of the half-hearted individuals cannot be more than the actual answer, and the answers of the enthusiastic individuals cannot be less than the actual number, determine the number of enthusiastic inhabitants within the group.
Solution 6
Line the inhabitants in a row according to their answers: 3 4 5 6 7 8 9 10 11 12. The first thing to note is that no half hearted person can be to the right of an enthusiastic person, so the half-hearteds are on the left.
Let’s say there are exactly 3 enthusiastic people. If this were so, the person who said ‘4’ must be enthusiastic, as must everyone to their right, totalling 9 enthusiastic people. Contradiction! So we can eliminate the solution being exactly 3 enthusiastic inhabitants.
Let’s say there are exactly 4 enthusiastic inhabitants. Again this leads to contradiction because it would mean there are at least 8 enthusiastic inhabitants. (The people to the right of the person who said ‘4’)
Likewise, it is impossible for there to be 5 enthusiastic inhabitants, as this implies at least 7 enthusiastic inhabitants.
If there are 6 enthusiastic people, there are no contradictions. But if there are 7 or more enthusiastic people, then it is impossible, since it would mean that some of these enthusiastic people are giving answers of less than 7, so this is impossible.
Thus there are 6 enthusiastic people.
2. Edgy logo (Ages 11/12)
The task here is to design a 2D logo using only equilateral triangles and squares, each with a side length of 1 cm. The triangles and squares must be glued together along their entire sides without any overlap.
Make a logo with a perimeter of 13 cm from the following shapes or prove it is impossible:
a) A single triangle and some squares
b) The same number of squares and triangles.
c) Only triangles.
d) Only squares.
Solution
a)

b)

c)

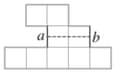
d) It’s impossible. When you make an object with only squares, all perimeter values are even, since every edge must have a corresponding edge on the other side of the shape, as in a and b here.
3. Axehead tiles (Ages 15/16)

The edges of these identical tiles are quarter circles, and their centres are the points marked. Determine the area of a tile, measured in cm2, given that the height of a standing tile is 12cm.
Solution 72
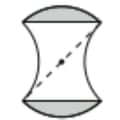
The top of a standing tile is a quarter circle, the centre of which is the centre of the tile, therefore the radius of the quarter circle is 6cm, and the corners of the tile are also 6 cm from the centre of the tile.
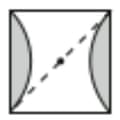
We can dissect the tile by removing the circle segments at the top and the bottom and placing them at the empty places on the left and right sides of the tile. We get a square with a diagonal of 12 cm. If the side length of the square is s, by Pythagoras’s Theorem we have: s2 + s2 = 122. Thus s2 = 72 = the area of the square = the area of the tile.
Today’s puzzles were taken from the Dürer Competition, a maths contest for 10 to 18 year olds that has been running in Hungary since 2007. If you liked them, there are many more in Mathematical Explorations for Young Minds.

I’m the author of Think Twice: Solve the Puzzles That (Almost) Everyone Gets Wrong, a collection of counter-intuitive conundrums that make you think about thinking – while enjoying the pleasure of being misled. The questions are not ‘trick’ questions; instead, they reveal our biases and flawed reasoning.
Think Twice: Solve the Simple Puzzles (Almost) Everyone Gets Wrong. To support the Guardian and Observer, order your copy at guardianbookshop.com. Delivery charges may apply. (In the US, the book is called Puzzle Me Twice.)
I’ve been setting a puzzle here on alternate Mondays since 2015. I’m always on the look-out for great puzzles. If you would like to suggest one, email me.

.png) 1 month ago
6
1 month ago
6













































